在上一篇文章中，我们介绍并分析了FTL算法，发现FTL算法在在线二次规划问题上能够获得还不错的效果，但是FTL算法的设计太简单，对于许多问题还无法得到好的结果，接下来，我们将给出一个例子，并分析FTL算法在这个例子上的表现，从而引出FTRL算法，并且从FTRL算法引出下面一篇将要分析的OGD算法。

The Failure Of FTL

下面我们将给出一个有关在线线性优化的例子，并推出FTL在这个例子上的Regret Bound。

在这个例子中，解空间$S =[-1,1]\in R$并且$t$轮的损失函数满足

$f_t(w)=z_t w$, \(z_t= \begin{cases}-0.5 & \text { if } t=1 \\ 1 & \text { if } t \text { is even } \\ -1 & \text { if } t>1 \wedge t \text { is odd }\end{cases}\)

那么，对于这样一个问题 ，其实我们可以看到，当运用FTL算法来预测就会出现当$t$为偶数时$\mathbf{w_t}$会被预测为1，而当$t$为奇数时$\mathbf{w_t}$就会被预测为-1，可以看到，$T$轮的累计损失为$T$，而$\min_{\mathbf{u} \in S} \sum_{t=1}^T f_t(\mathbf{u})$为0，所以该算法在这个问题上的Regret Bound就会到 T ，可以看到此时这个算法的效果就不好了，它在每一轮都和实际的结果不同。那为什么FTL算法在上面的例子中表现得效果就不好了呢？直观上分析，上面的例子中每一轮的损失函数变化的幅度太大了，而我们的FTL算法又只在每次预测时考虑最小化过去的损失和，这样就会太收过去的影响，从而过于拟合过去的数据，就像在传统学习中的过拟合问题一样。就像传统学习中利用正则化项解决过拟合问题一样，我们在FTL的算法中加入正则化项，也就有了Follow-The-Regularized-Leader (FTRL)算法。下面将介绍FTRL算法。

FTRL

FTRL在FTL的基础上加入了正则化项$R(\mathbf{w})$。用数学具体表示就是：

$\forall t, \quad \mathbf{w_t}=\underset{\mathbf{w} \in S}{\operatorname{argmin}} \sum_{i=1}^{t-1} f_i(\mathbf{w})+R(\mathbf{w})$

根据加入正则化项的不同，也有了不同的具体算法。当我们对在线线性优化问题上（损失函数$f_t(\mathbf{w_t})=<\mathbf{w_t},\mathbf{z_t}>$）用正则化项$R(\mathbf{w})=\frac{1}{2 \eta}\Vert\mathbf{w}\Vert_2^2$，并且解空间$S$为$R^d$时，我们就可以得出：

$\mathbf{w_{t+1}}=\mathbf{w_t}-\eta \mathbf{z_t}$

注意$\mathbf{z_t}$可以被写为$\nabla f_t\left(\mathbf{w_t}\right)$，也就是可以写作

$\mathbf{w_{t+1}}=\mathbf{w_t}-\eta\nabla f_t\left(\mathbf{w_t}\right)$

从这个形式，我们可以看出，这和凸优化算法中的梯度下降法是一样的。这也启发我们后面设计出Online Gradient Decent算法。

接下来，我们先对FTRL这个general的框架进行一定的分析。

Regret Bound

同分析FTL一样，我们先将Regret转化为更容易计算的式子。对于FTRL，有下面的引理成立：

$\mathbf{w_1},\mathbf{w_2},…$是FTRL预测的结果，对于任意一个$\mathbf{u}∈S$,都有

$\sum_{t=1}^T\left(f_t\left(\mathbf{w_t}\right)-f_t(\mathbf{u})\right) \leq R(\mathbf{u})-R\left(\mathbf{w_1}\right)+\sum_{t=1}^T\left(f_t\left(\mathbf{w_t}\right)-f_t\left(\mathbf{w_{t+1}}\right)\right)$

可以发现，运行FTRL算法其实和运行加上一个损失函数$f_0=R(\mathbf{w})$的FTL是一样的。利用FTL的分析，我们就可以得到$\sum_{t=0}^T\left(f_t\left(\mathbf{w_t}\right)-f_t(\mathbf{u})\right) \leq \sum_{t=0}^T\left(f_t\left(\mathbf{w_t}\right)-f_t\left(\mathbf{w_{t+1}}\right)\right)$，利用$f_0=R(\mathbf{w})$再重新整理，就可以得到要证明的引理了。

利用上面证明的引理，我们可以对之前提出的在线线性优化问题进行分析，得到其Regret Bound。对于任意一个$\mathbf{u}∈S$,都有

$\operatorname{Regret_T}(FTRL) \leq \frac{1}{2 \eta}\Vert\mathbf{u}\Vert_2^2+\eta \sum_{t=1}^T\Vert\mathbf{z_t}\Vert_2^2$

特别的，当我们假设$u$始终满足$|\mathbf{u}| \leq B$，有$L$满足$\frac{1}{T} \sum_{t=1}^T\Vert\mathbf{z_t}\Vert_2^2 \leq L^2$并且将$η$设为$\frac{B}{L \sqrt{2 T}}$时，我们就有了下面的更直观的不等式：

$\operatorname{Regret_T}(FTRL) \leq B L \sqrt{2 T}$

证明过程比较简单，只要用到之前推出的$\mathbf{w_{t+1}}=\mathbf{w_t}-\eta \mathbf{z_t}$和上面证明的引理，就很容易得到：

\[\begin{aligned} \operatorname{Regret_T}(FTRL) & \leq R(\mathbf{u})-R\left(\mathbf{w_1}\right)+\sum_{t=1}^T\left(f_t\left(\mathbf{w_t}\right)-f_t\left(\mathbf{w_{t+1}}\right)\right) \\ &=\frac{1}{2 \eta}\Vert\mathbf{u}\Vert_2^2+\sum_{t=1}^T\langle\mathbf{w_t}-\mathbf{w_{t+1}}, \mathbf{z_t}\rangle \\ &=\frac{1}{2 \eta}\Vert\mathbf{u}\Vert_2^2+\eta \sum_{t=1}^T\Vert\mathbf{z_t}\Vert_2^2 . \end{aligned}\]

可以看到，该算法在一般的线性回归问题中表现得还不错，Regret Bound为次线性的。但是其实，算法设计很好，实际运行当中却有一定的问题，那就时我们在设计步长时，参数中有总的轮数$T$,但在实际中，我们是得不到这个$T$的值的，所以我们需要用一个简单的技巧来避开这个问题，那就是接下来要介绍的The Doubling Trick。

The Doubling Trick

The Doubling Trick，简单来说就是将整个训练的时间分为递增大小的时期，在每个时期上运行算法。具体表示如下：

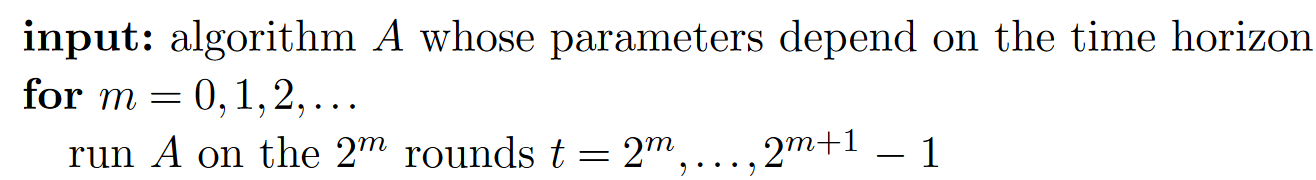
假设该算法$A$的Regret Bound可以写为为$α_T$,那么在每个轮数为$2^m$的时期上的Regret最多为$\alpha \sqrt{2^m}$，因此可以分析出：

\[\begin{aligned} \sum_{m=1}^{\left\lceil\log_2(T)\right\rceil} \alpha \sqrt{2^m} &=\alpha \sum_{m=1}^{\left\lceil\log_2(T)\right\rceil}(\sqrt{2})^m \\ &=\alpha \frac{1-\sqrt{2}^{\left\lceil\log_2(T)\right\rceil+1}}{1-\sqrt{2}} \\ & \leq \alpha \frac{1-\sqrt{2 T}}{1-\sqrt{2}} \\ & \leq \frac{\sqrt{2}}{\sqrt{2}-1} \alpha \sqrt{T} . \end{aligned}\]

可以看出，虽然Regret Bound大了一点，但是却有效的避免了无法实现的问题。