在上一篇文章中，我们介绍了FTL算法的改进版本FTRL算法，同时在分析FTRL算法对线性损失函数的情况中看到了像Gradient Decent算法一样形式的参数更新式子，我们接下来就介绍一个将凸函数线性化分析的方法，并用这个方法去将我们之前的分析推广。

Linearization of Convex Functions

下面我们将介绍一种在凸优化中很常见也很有用的线性化分析方法。首先，对于凸函数 f ，我们有以下这个定理成立

定理一：$\forall \mathbf{u} \in S, \quad f(\mathbf{u}) \geq f(\mathbf{w})+\langle\mathbf{u}-\mathbf{w}, \mathbf{z}\rangle$

其中，$S$为函数的定义域，$\mathbf{u}$和$\mathbf{w}$都是定义域$S$中的任意一个取值，$\mathbf{z}$是函数$f$在$\mathbf{w}$处的梯度。

这个定理也是凸函数的基本定义之一，显然是很容易理解的。

但是，在用这个定理的时候，我们需要将梯度求出，可有的时候函数是不可导的，梯度无法被求出，所以，为了应对这种情况，我们可以将梯度换为次梯度来进行分析。

下面介绍次梯度的定义：

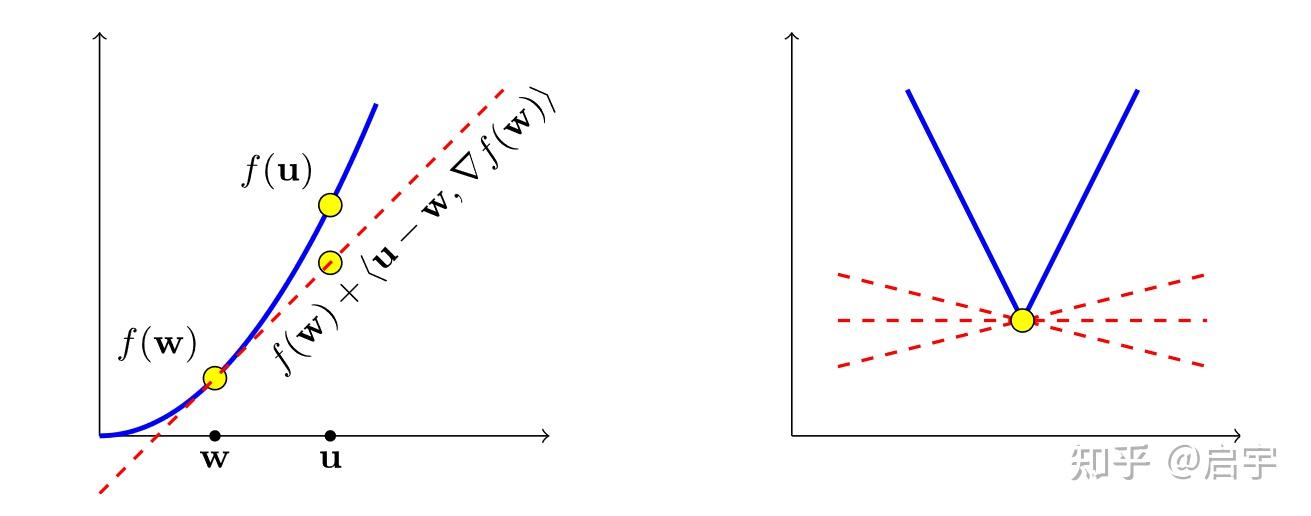
满足上面给出的定理一不等式的向量$\mathbf{z}$都被称为这个函数$f$在$\mathbf{w}$处的次梯度。由于满足上面的不等式的向量不止一个，我们将他们的集合写作$\partial f(\mathbf{w})$。下面给出一个形象的图片来说明

利用以上说明的定理，我们就可以对凸函数进行一定的线性简化分析。

$Regret=\sum_{t=1}^T\left(f_t\left(\mathbf{w_t}\right)-f_t(\mathbf{u})\right) \leq \sum_{t=1}^T\left(\left\langle\mathbf{w_t}, \mathbf{z_t}\right\rangle-\left\langle\mathbf{u}, \mathbf{z_t}\right\rangle\right)$

其中，$\mathbf{u}$满足$\mathbf{u}=argmin(\sum_{t=1}^Tf_t(\mathbf{u}))$。

这样的话，原来非线性的函数就可以利用线性的分析来推出Regret Bound。下面，我们将利用这一点，引出OGD算法，并对其利用之前FTRL的分析来证明出一个Regeret Bound。

Online Gradient Decent (OGD)

先介绍OGD算法：

利用之前对OGD的线性化，并结合上一篇文章对FTRL算法在线性函数上的分析，可以得出下面的这个结论

$\operatorname{Regret_T}(\mathbf{u}) \leq \frac{1}{2 \eta}\Vert\mathbf{u}\Vert_2^2+\eta \sum_{t=1}^T\left\Vert\mathbf{z_t}\right\Vert_2^2$

为了得出一个更加精确的Regret Bound，我们对函数进行一个限制，一般我们规定函数的次梯度不是无穷大的，其中一种方法就是利用Lipschitz连续来限制。

下面有这样一个定理，他揭示了函数Lipschitz连续和对偶范数之间的关系。

（有关Lipschitz连续和对偶范数的详细介绍，后面我可能会专门写一个专栏来介绍。）

定理二：$f: S \rightarrow \mathbb{R}$是一个凸函数，那么函数$f$在$S$上是有关范数$|\mathbf{.}|$L-Lipschitz连续的，等价于对于所有$\mathbf{w}∈S$且任意一个$\mathbf{z} \in \partial f(\mathbf{w})$都有$\mathbf{z}$的上述范数的对偶范数满足$\Vert\mathbf{z}\Vert_{\star} \leq L$。

再证明必要性。根据次梯度，有

$f(\mathbf{w})-f(\mathbf{u}) \leq\langle\mathbf{z}, \mathbf{w}-\mathbf{u}\rangle$

又根据对偶范数定义，有如下不等式成立

$\langle\mathbf{z}, \mathbf{w}-\mathbf{u}\rangle\ \leq \Vert\mathbf{z}\Vert_{\star}\Vert\mathbf{w}-\mathbf{u}\Vert$

则结合$\Vert\mathbf{z}\Vert_{\star} \leq L$可推得

$f(\mathbf{w})-f(\mathbf{u}) \leq\Vert\mathbf{z}\Vert_{\star}|\mathbf{w}-\mathbf{u}| \leq L|\mathbf{w}-\mathbf{u}|$

故函数$f$是L-Lipschitz连续的。

有了定理二，我们就可以对OGD算法进行进一步的分析。由于二范数的对偶范数就是自身，那么我们可以得到

当$f_t$是$L_t$-Lipschitz连续的时候，有

$\sum_{t=1}^T\Vert\mathbf{z_t}\Vert_2^2 \leq \sum_{t=1}^T L_t^2$

故可以从之前推出的Regret Bound进一步得出

$\operatorname{Regret_T}(\mathbf{u}) \leq \frac{1}{2 \eta}\Vert\mathbf{u}\Vert_2^2+\eta T L^2$

当$\mathbf{u}$满足$\Vert\mathbf{u}\Vert_2 \leq B$时，并且选择$\eta=\frac{B}{L \sqrt{2 T}}$，便有了

$\operatorname{Regret_T}(\mathbf{u}) \leq B L \sqrt{2 T}$

可以看到，这个有关$T$的函数是次线性的，这个算法的理论保障被证明。